Chapter 12 Chapter 12: influenceR package
In this chapter, we explore two additional micro-level network metrics that are developed in the domain of social network analysis. For this, we need to install the influenceR R package which provides the functions for computing bridging scores and effective network sizes for nodes in the network.
12.1 Set up
First, let’s install the influenceR R package:
We will continue to use the macaque network from Chapter 11 for demonstration.
library(igraphdata)
data("macaque")
# load the other packages that we need
library(igraph)
library(influenceR)##
## Attaching package: 'influenceR'## The following objects are masked from 'package:igraph':
##
## betweenness, constraint# to make edges undirected by collapsing directed edges
macaque <- as.undirected(macaque, mode = 'collapse')## Warning: `as.undirected()` was deprecated in igraph 2.1.0.
## ℹ Please use `as_undirected()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.## This graph was created by an old(er) igraph version.
## ℹ Call `igraph::upgrade_graph()` on it to use with the current igraph version.
## For now we convert it on the fly...12.2 Bridging score
Granovetter (1973) observed that edges that reduce the overall distance of a network are structurally important bridges. These are usually the “weak” edges in a social network where the nature of the relationship between those two individuals are on an acquaintance basis. Nevertheless, the presence of these edges enable connection between distant parts of the network.
Valente and Fujimoto (2010) built on that insight and developed a “node-centric” measure of bridging that considers the impact of deleting an edge or link on the cohesiveness of the network. In other words, a node with a higher bridging score tends to possess a structurally important edge, such that deleting it substantially reduces the overall connectivity of the network.
A node’s bridging score, \(B_i\), is the average decrease in cohesiveness when each of its edges are systematically removed from the graph.
\(B_i=\frac{∑ΔC}{k_i}\)
where \(k_i\) = the degree of node i and \(ΔC\) = change in network cohesiveness.
For each connected edge of a target node:
- Remove the edge and recompute network cohesiveness (inverse of distance)
- Take the difference from the original network cohesiveness (i.e., the decrease)
Then, take the sum of the change in cohesiveness, divide by the number of edges (degree).
Below, we can easily use the bridging function to compute this information for us.
## V1 V2 V3 V3A V4 V4t VOT VP MT MSTd/p MSTl PO LIP PIP VIP
## 0.0003156566 0.0003310887 0.0002976190 0.0003108003 0.0005071549 0.0003282828 0.0002693603 0.0002976190 0.0002946128 0.0002921371 0.0003328742 0.0002861953 0.0003135522 0.0003507295 0.0005250922
## DP 7a FST PITd PITv CITd CITv AITd AITv STPp STPa TF TH FEF 46
## 0.0003086420 0.0003900112 0.0002702463 0.0003367003 0.0002840909 0.0004349046 0.0003682660 0.0003198653 0.0003848004 0.0003661616 0.0004377104 0.0004307784 0.0003437149 0.0003979186 0.0004861111
## 3a 3b 1 2 5 Ri SII 7b 4 6 SMA Ig Id 35 36
## 0.0004349046 0.0004629630 0.0003787879 0.0003749617 0.0003979186 0.0004103535 0.0005536131 0.0003561254 0.0003114478 0.0003137435 0.0003156566 0.0004278900 0.0004945286 0.0005471380 0.0005611672bridging_data <- data.frame(node = V(macaque)$name,
bridge_score = bridging(macaque))
head(bridging_data)## node bridge_score
## V1 V1 0.0003156566
## V2 V2 0.0003310887
## V3 V3 0.0002976190
## V3A V3A 0.0003108003
## V4 V4 0.0005071549
## V4t V4t 0.000328282812.2.1 Important note about directed graphs
The bridging function does not work as expected when edges are directed. Negative scores and inconsistent scores could arise from running this function on graphs with directed edges. Hence, please convert directed graphs into undirected graphs before proceeding (see Chapter 5.5, as.undirected() function). The root cause of this is because of a parallelization invoked in the function to compute the change in the cohesion when removing each edge, which does not behave consistently when edges are directed.
12.3 Effective network science
Burt (2004) argues that people who are located near “holes” in a social network tend to have better ideas. This occurs because such individuals are “brokers” across different social groups and can accumulate social capital more quickly.
The effective size of a node’s ego network is based on the concept of redundancy. A person’s ego network has redundancy to the extent that their contacts are connected to each other as well. The nonredundant part of a person’s relationships is the effective size of their ego network. The maximum ENS is the degree of the ego. The minimum ENS is 1, as if one “effectively” only had 1 single friend.
A node’s effective network size, \(E_i\), is computed as follows:
\(E_i=k−2t/k\)
where t = number of ties in the ego network and k = the degree of the node.
For each node:
- Extract the ego network of the node. The ego network is the immediate neighborhood of the node.
- Check the extent to which its neighbors are connected by counting number of ties, t.
Below, we can easily use the ens function to compute this information for us.
## V1 V2 V3 V3A V4 V4t VOT VP MT MSTd/p MSTl PO LIP PIP VIP DP 7a FST PITd PITv
## 2.000000 6.200000 5.428571 4.076923 12.900000 3.200000 3.000000 6.000000 6.125000 7.941176 4.272727 5.933333 10.700000 3.888889 12.333333 4.833333 8.866667 10.157895 5.250000 6.666667
## CITd CITv AITd AITv STPp STPa TF TH FEF 46 3a 3b 1 2 5 Ri SII 7b 4 6
## 3.000000 3.750000 5.600000 3.000000 6.400000 1.800000 11.941176 7.333333 13.454545 13.900000 2.000000 1.000000 2.750000 4.636364 5.181818 1.500000 7.615385 6.538462 4.200000 4.272727
## SMA Ig Id 35 36
## 2.750000 4.000000 2.500000 3.000000 4.666667## node ens_score
## V1 V1 2.000000
## V2 V2 6.200000
## V3 V3 5.428571
## V3A V3A 4.076923
## V4 V4 12.900000
## V4t V4t 3.200000By now, you should know how to export the data frames as a .csv file for further exploration! (Hint: write.csv(...)).
12.3.1 How is effective network science different from local clustering coefficient?
A common question that arises is whether ENS is really capturing information that is different from that of local clustering coefficient (Chapter 7.3), since both measures are micro-level network measures that quantify the density of the internal connectivity structure of a node’s immediate neighbors. To illustrate how they are different we consider two toy networks (visualized below). For the first network we are interested in ego node 1, which has a degree of 5, and for the second network we are interested in ego node 21, which has a degree of 20.
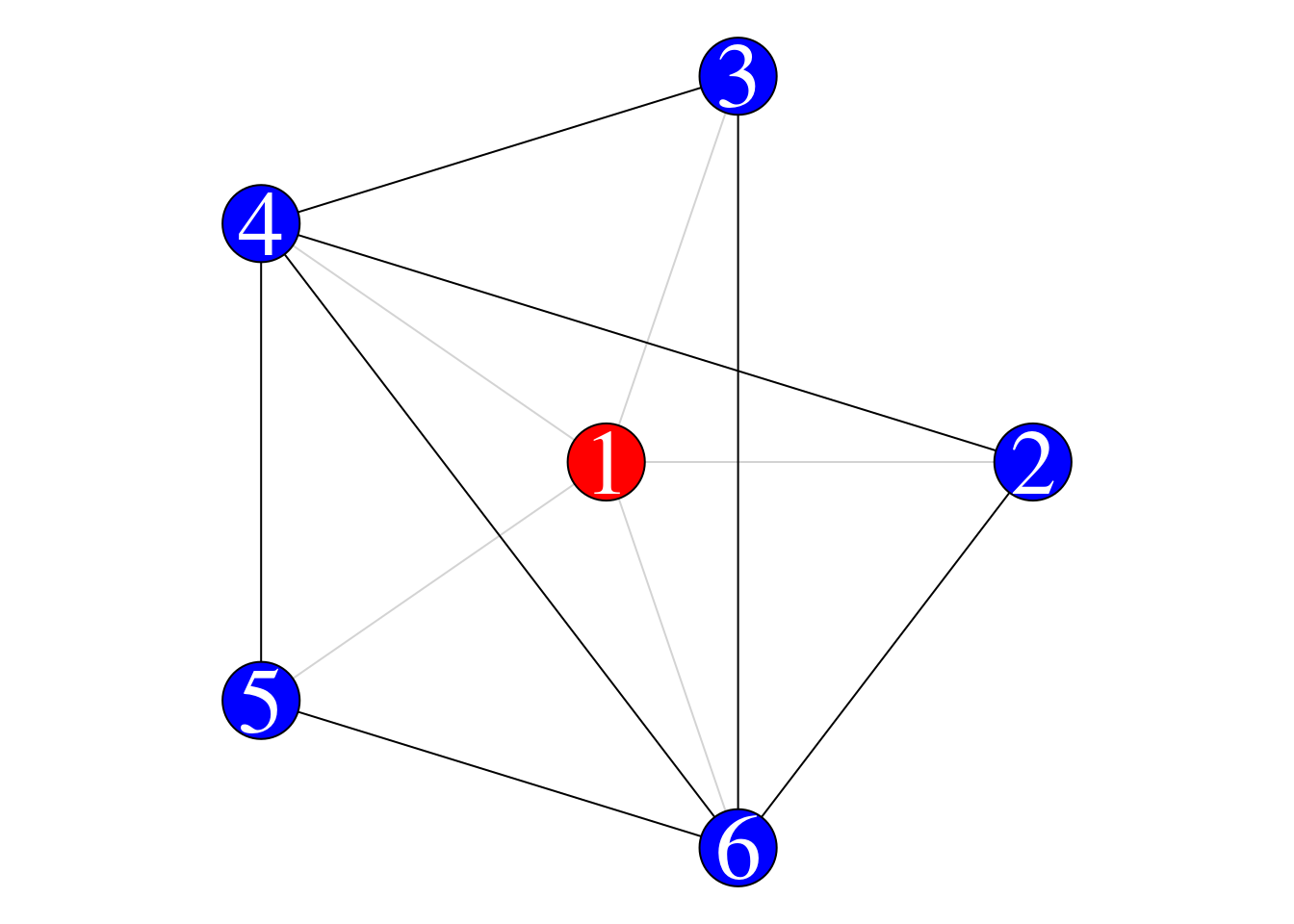
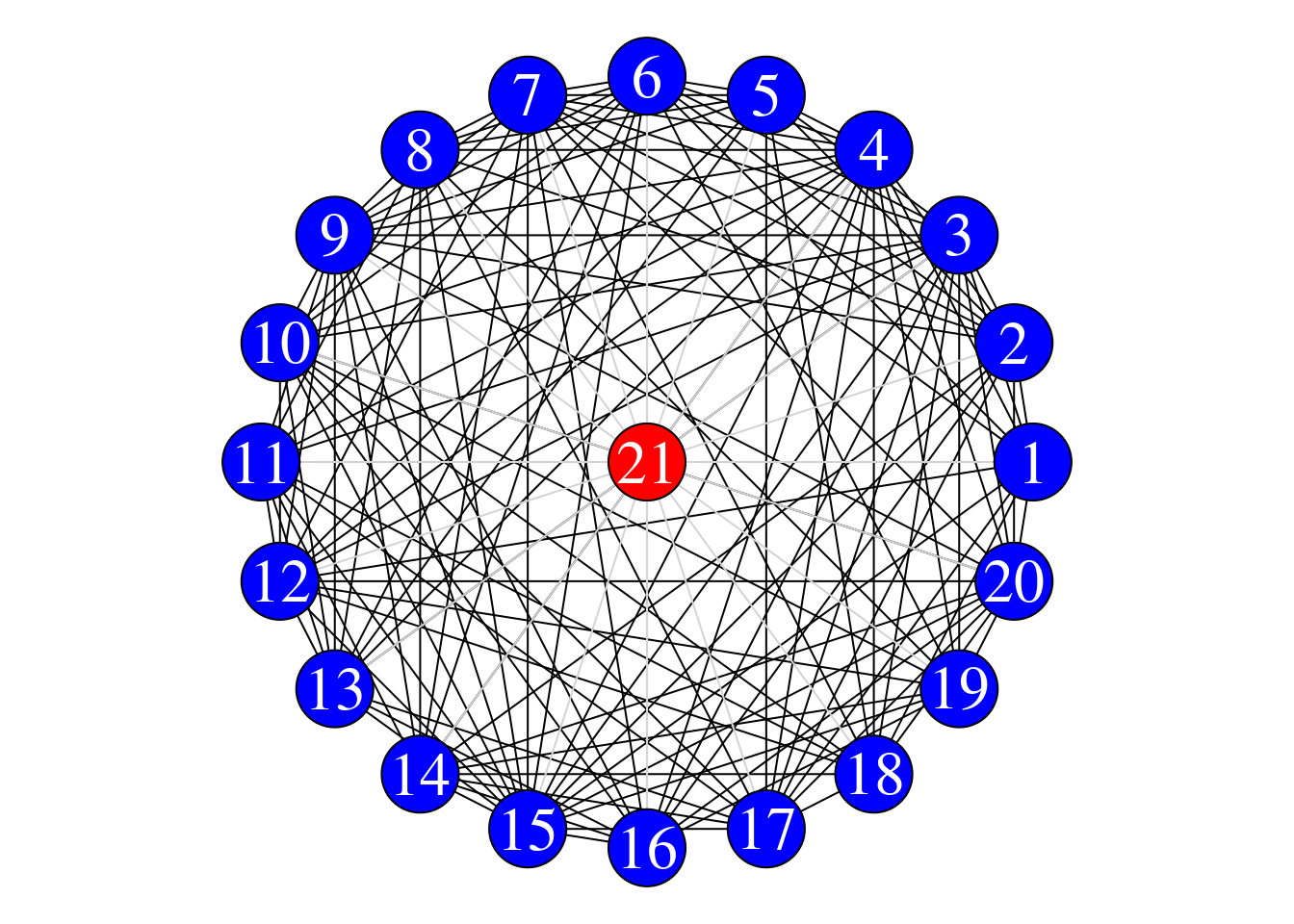
Let’s compute the ENS and local C for the ego node in the smaller neighborhood (using both the corresponding functions and the mathematical equations):
## [1] 0.7## [1] 0.7## [1] 2.2## [1] 2.2Let’s also compute the ENS and local C for the ego node in the larger neighborhood (using both the corresponding functions and the mathematical equations):
## 21
## 0.7## [1] 0.7## 21
## 6.7## [1] 6.7What you will notice is that although both nodes have a local C of 0.7, indicating that 70% of all possible connections in their immediate neighborhoods are fulfilled, the two nodes have different effective network sizes. The node from the larger neighborhood has a ENS of 6.7 whereas the node from the smaller neighborhood has a ENS of 2.2. The difference in ENS reflects the fact that the node from the larger neighborhood has more potential in its ability to fill/exploit structural holes in their network than the node from the smaller neighborhood, due to the former having a larger neighborhood to begin with. This is despite both nodes having the same level of interconnectivity within their neighborhoods.
12.3.2 Important note about directed graphs
The ens function does not work as expected when edges are directed. Negative scores and scores less than 1 could arise from running this function on graphs with directed edges. Hence, please convert directed graphs into undirected graphs before proceeding (see Chapter 5.5, as.undirected() function).
12.4 References
Burt, R. S. (2004). Structural holes and good ideas. American Journal of Sociology, 110(2), 349-399.
Granovetter, M. S. (1973). The strength of weak ties. American Journal of Sociology, 78(6), 1360-1380.
Valente, T. W., & Fujimoto, K. (2010). Bridging: locating critical connectors in a network. Social Networks, 32(3), 212-220.
12.5 Exercise
Conduct the following analysis on a social network of your choosing, where the nodes correspond to individual persons. If you do not have a social network, you could conduct the analysis on the karate or UKfaculty networks from the igraphdata library.
- Identify the individuals with the highest and lowest bridging scores.
- What is the implication of having a high bridging score for this particular network?
- What is the implication of having a low bridging score for this particular network?
- Identify the individuals with the highest and lowest effective network sizes.
- What is the implication of having a high effective network size for this particular network?
- What is the implication of having a low effective network size for this particular network?